Sortieralgorithmen
Bubblesort
Video - Bubblesort
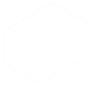
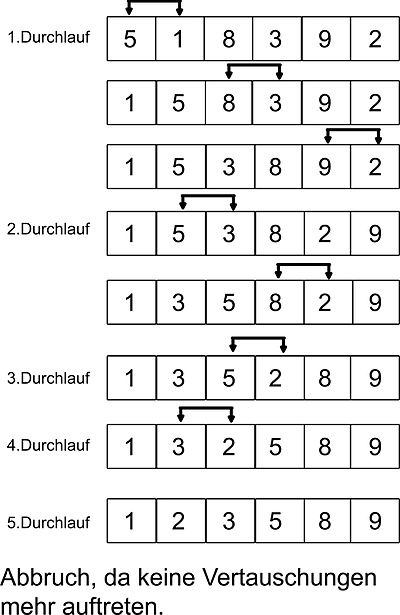
Beim Bubblesort Algorithmus wird ein Array – also eine Eingabe-Liste – immer paarweise von links nach rechts in einer sogenannten Bubble-Phase durchlaufen. Man startet also mit der ersten Zahl und vergleicht diese dann mit ihrem direkten Nachbarn nach dem Sortierkriterium. Sollten beide Elemente nicht in der richtigen Reihenfolge sein, werden sie ganz einfach miteinander vertauscht. Danach wird direkt das nächste Paar miteinander verglichen, bis die gesamte Liste einmal durchlaufen wurde. Die Phase wird so oft wiederholt, bis der gesamte Array vollständig sortiert ist.
Insertionsort
Video - Insertionsort
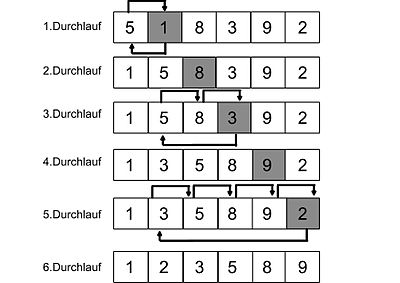
Der Insertion Sort gehört in der Informatik zu den stabilen Sortieralgorithmen und kann als Sortieren durch Einfügen beschrieben werden, deswegen auch Einfügesortierenmethode genannt. Das Ganze lässt sich natürlich einfach durch die englischen Wörter insertion = Einfügen und sort = sortieren ableiten, weswegen der Sortieralgorithmus auch manchmal als Insertsort bezeichnet wird. Allgemein kann auch noch gesagt werden, dass der Sortieralgorithmus einfach zu implementieren ist und dabei bei kleiner oder schon teilweise vorsortierten Eingabemengen sehr effizient arbeitet. Da das Sortierverfahren keinen zusätzlichen Speicherplatz benötigt, arbeitet der Algorithmus in-place, was natürlich für seine Speicherplatzkomplexität spricht.
Quicksort
Video - Quicksort
Zunächst wird die zu sortierende Liste in zwei Teillisten („linke“ und „rechte“ Teilliste) getrennt. Dazu wählt Quicksort ein sogenanntes Pivotelement aus der Liste aus. Alle Elemente, die kleiner als das Pivotelement sind, kommen in die linke Teilliste, und alle, die größer sind, in die rechte Teilliste. Die Elemente, die gleich dem Pivotelement sind, können sich beliebig auf die Teillisten verteilen. Nach der Aufteilung sind die Elemente der linken Liste kleiner oder gleich den Elementen der rechten Liste.
Anschließend muss man also noch jede Teilliste in sich sortieren, um die Sortierung zu vollenden. Dazu wird der Quicksort-Algorithmus jeweils auf der linken und auf der rechten Teilliste ausgeführt. Jede Teilliste wird dann wieder in zwei Teillisten aufgeteilt und auf diese jeweils wieder der Quicksort-Algorithmus angewandt, und so weiter. Diese Selbstaufrufe werden als Rekursion bezeichnet. Wenn eine Teilliste der Länge eins oder null auftritt, so ist diese bereits sortiert und es erfolgt der Abbruch der Rekursion.
Die Positionen der Elemente, die gleich dem Pivotelement sind, hängen vom verwendeten Teilungsalgorithmus ab. Sie können sich beliebig auf die Teillisten verteilen. Da sich die Reihenfolge von gleichwertigen Elementen zueinander ändern kann, ist Quicksort im Allgemeinen nicht stabil.
Das Verfahren muss sicherstellen, dass jede der Teillisten mindestens um eins kürzer ist als die Gesamtliste. Dann endet die Rekursion garantiert nach endlich vielen Schritten. Das kann z. B. dadurch erreicht werden, dass das ursprünglich als Pivot gewählte Element auf einen Platz zwischen den Teillisten gesetzt wird und somit zu keiner Teilliste gehört.
Mergesort
Video - Mergesort
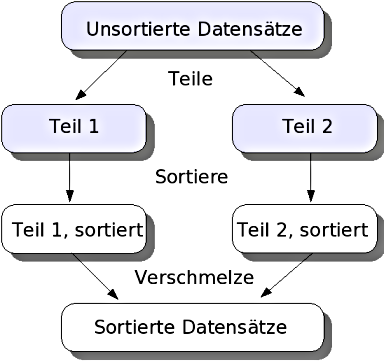
Mergesort betrachtet die zu sortierenden Daten als Liste und zerlegt sie in kleinere Listen, die jede für sich sortiert werden. Die kleinen sortierten Listen werden dann im Reißverschlussverfahren zu größeren sortierten Listen zusammengefügt, bis eine sortierte Gesamtliste erreicht ist. Das Verfahren arbeitet bei Arrays in der Regel nicht in-place, es sind dafür aber Implementierungen bekannt, in welchen die Teil-Arrays üblicherweise rekursiv zusammengeführt werden. Verkettete Listen sind besonders geeignet zur Implementierung von Mergesort, dabei ergibt sich die in-place-Sortierung fast von selbst.